GDot Home
In 1884 P.G. Tait conjectured that every polyhedral graph has a Hamilton cycle. The conjecture was disproved more than 60 years laterby Tutte, using the graph in below. The picture clearly shows the automorphism group of the graph as rotational symmetries in the picture. The nodes are clustered in the picture by their orbits (i.e., equivalence classes under automorphism). In between the outer face and the central node are three mutually isomorphic subgraphs, called “Tutte fragments”. These fragments are critical to the proof that the graph has no Hamilton cycle. A simple mathematical argument, based on the orbits and the “Tutte fragments”, shows that the graph has no Hamilton cycle.
-
-
-
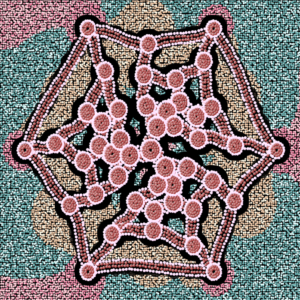
Tutte_01 -

Tutte_02
-
-

